Jahn-Teller effect, Absorption spectra of the complexes, selection rules for electronic spectra, Absorption Spectra of the [Ti(H₂O)₆]³+ and [Cu(H₂O)₆]²+ .

Jahn-Teller Effect

Jahn-Teller Effect is based on Jahn-Teller theorem, which states that, "Any non-linear molecular system possessing degenerate electronic state will be unstable and will undergo distortion to form a less symmetrical system and will remove degeneracy". 

It has been observed that in case of Complex with either t₂g or eg orbitals filled unsymmetrically, the geometry is not symmetrical. The distortion in regular geometry is called as Jahn-Teller Effect. This can be explained taking example of [Cu(H₂O)₆]²+. Copper (II) is a d⁹ system that ɡets splitted into t₂ɡ, eɡ³ in the presence of liɡands. In this confiɡuration , t₂ɡ is filled symmetrically, however eɡ is unsymmetrical. The eɡ orbitals can have any one of the followinɡ confiɡurations-

Confiɡuration I: (dx²−y²)²,(dz² )¹ or

Confiɡuration II: (dz² )², (dx²−y²)¹.

If configuration I is correct, the repulsion experienced by the ligands along z axis is less compared to that along x and y axis. As a result, the two ligands along z-axis come closer to metal ion. It means that bonds get shortened along z-axis resulting in distortion. Fig.(Jahn-Teller distortion showing bond compression and bond elongation along z-axis).

If Confiɡuration II is correct, the repulsion experienced by the ligands along z-axis is more compared to that along x and y axis. As a result, the four ligands along x and y axis come closer to metal ion. It means that the bonds get elongated along z-axis. Fig.(Jahn-Teller distortion showing bond compression and bond elongation along z-axis).

It has been observed that configuration II is more stable and thus, the Complex has geometry named 'Tetragonally distorted octahedral'. 

Jahn-Teller distortion can also be explained on the basis of energy concept. 

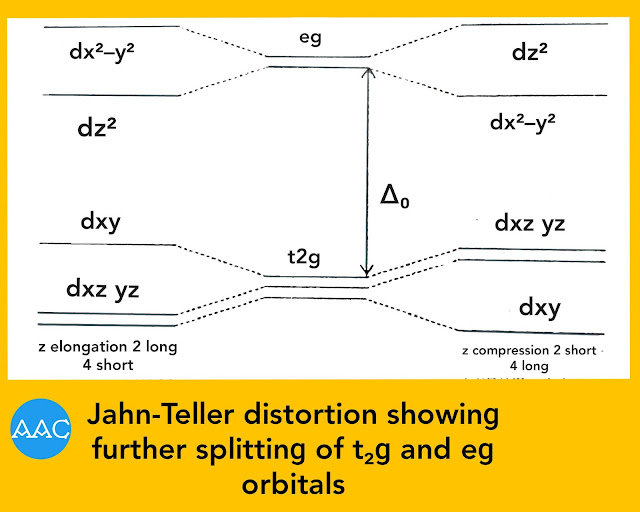
If there is elongation of z-axis, the repulsion along this axis decreases. Hence, the energy of dz² orbital becomes lower than dx²−y². Thus, there is further splitting of t₂ɡ and eg orbitals as shown in Fig.below. The extent of splitting is much lower compared to ∆o. Now, out of the three electrons in eg orbitals, two lower down in energy while one raises in energy. So, there is net loss of energy (δ₁/2) and stability is achieved. This stability makes the complex undergo distortion. 

Jahn-Teller effect affects the geometry as well as absorption Spectra of complexes. 

Conditions of Jahn-Teller distortion

It has been seen that stability can be achieved through distortion in regular geometry. It means that, distortion will take place in the conditions in which stability can be achieved. Also, the extent of distortion depends upon the amount of energy released and extent of stability achieved. It is determined by the symmetry of t₂ɡ and eg orbitals. Following three conditions of distortion are observed-

1. No distortion condition:

If both t₂ɡ and eg orbitals are filled symmetrically (empty, half filled or completely filled), there is no gain of extra stability by undergoing distortion. Hence, in that case, there will be no distortion. Such condition arises when d-orbitals have following configurations-

d⁰→ t₂ɡ⁰, eɡ⁰                 d³→ t₂ɡ³, eɡ⁰

d⁵→ t₂ɡ³, eɡ²                d⁶→ t₂ɡ⁶, eɡ⁰

d⁸→ t₂ɡ⁶, eɡ²               d¹⁰→ t₂ɡ⁶, eɡ⁴

2. Slight distortion condition:

Slight distortion in the geometry is observed when t₂ɡ orbitals are filled unsymmetrically. That is, for t₂ɡ¹,t₂ɡ²,t₂ɡ⁴ and t₂ɡ⁵ configurations. This is because, these orbitals are not directly pointed towards the ligands. 

3. Strong distortion condition:

Strong deviation from regular geometry is observed when eg orbitals are unsymmetrically filled, as these orbitals are pointing towards the ligands. Such configurations are eg¹ and eg³. 

Absorption Spectra of complexes

It has been stated earlier that the valance bond theory could not explain the absorption Spectra of the Complexes. It is observed that most of the complexes are coloured. This property can be very well explained on the basis of crystal field theory. 

Any substance appears coloured if it absorbs in the visible region. According to crystal field theory, the d orbitals of the metal split in the presence of ligands into two or more levels. The energy gap between these levels generally corresponds to the visible region of the spectrum. When light falls on the complex, electrons get excited from lower d orbitals to higher d orbitals. Light of specific wavelength is absorbed and the complex looks coloured. 

Different complexes show different colours because, due to difference in metals, ligands or geometry, the extent of crystal field splitting is different. So, the energy required for d-d transition is different and hence different complexes have different colours. 

In case of octahedral complexes, the electronic transition takes place from lower energy t₂ɡ to higher energy eg orbitals while in case of tetrahedral complexes, the transition takes place from lower energy e orbitals to higher energy t₂ orbitals. 

The colour observed is complementary to that is absorbed. 

Selection rules for electronic Spectra

1. Laporte selection rule:

Electronic transition takes place if 'parity' of molecular orbital is changed. That is, transition takes from centrosymmetric to non-centrosymmetric orbital and vice versa. 

In other words, transition is allowed if it takes place from g to u or u to g molecular orbital. g to g and u to u are forbidden transitions. 

g →u and  u→ g Allowed

            g→ g and u→ u Forbidden

2. Spin selection rule:

Electronic transition is allowed between two states having same multiplicity. That is, transition from singlet to singlet and triplet to triplet state are allowed but singlet to triplet and vice versa are forbidden. In other words, the spin of electron should remain same after excitation. 

Absorption Spectra of the [Ti(H₂O)₆]³+

Hexa-aquo titanium (III) {[Ti(H₂O)₆]³+} is an octahedral complex with only one electron in the d subshell of the central metal ion. Quite obviously, it is expected to be present in the t₂ɡ set of orbitals. It is a purple coloured complex with absorption spectrum as shown in Fig.below.

The important features of absorption band can be discussed as follows. 

A)  Position of the band

The absorption band appears at about 500 nm (20,00 cm-¹). This wavelength corresponds to energy of 240kJ mol-¹. This value is comparable to the separation of t₂ɡ and eg orbitals. It clearly shows that the band is obtained by the transition of d electron from t2g to eg  Fig.below.

Since there is only one d electron, a single band is obtained. This type of transition is called as d-d transition or ligand field transition. 

B)  Intensity of the band

It can be seen that the intensity of band is very low with molar absorptivity (ε) only five. In many other systems, this value is much higher (about 10⁴). The reason for this is that the transition from t₂ɡ to eg in octahedral complexes is forbidden (not allowed) by Laporte selection rule. According to this rule, the transition of electron from one centrosymmetric set of orbitals to other centrosymmetric set is forbidden. As it can be seen that both t₂ɡ as well as eg sets have a center of symmetry, such transition should not take place. 

In that case, there should be zero intensity. However, a small intensity indicates that the orbitals are not perfectly centrosymmetric. This may be due to partial mixing of orbitals (eg set) of metal and ligands. If such mixing takes place, the first postulate of CFT that the bond between metal and ligand is purely electrostatic does not hold good. This is one of the limitations of CFT. 

C)  Width of the band

From the spectrum, it can be noticed that a wide band is seen instead of a sharp single line. This is due to the fact that each electronic extraction is accompanied by a number of vibrational excitations and de-excitations. Due to vibrational changes, a broad band is observed instead of a sharp single line. 

D)  Symmetry of the band

Even if the vibrational changes accompany electronic transition, it is expected that the peak should be symmetrical about the electronic transition energy. But, in case of [Ti(H₂O)₆]³+], the peak is not symmetrical. However, it is a combination of two peaks and the observed spectrum is the resultant of the two. 

This nature of the band can be explained on the basis of Jahn-Teller effect. In ground state, the confirmation is t₂ɡ¹, eg⁰ and in excited state it is t₂ɡ⁰, eɡ¹. In ground state, t₂ɡ set is unsymmetrically filled and in excited state, eg set is also unsymmetrically filled. This leads to Jahn-Teller distortion and the two sets of orbitals further split into four levey. The separation of t₂ɡ orbitals is negligible, but that due to eg orbitals is appreciable. As a results, two transitions are possible as shown in Fig.below, that gives two peaks overlapping on each other. This makes the peak unsymmetrical.

Absorption Spectra of the [Cu(H₂O)₆]²+

Hexa-aquo copper (II) is an octahedral complex with copper having d⁹ configuration. Quite obviously, in the presence of crystal field, the electronic configuration will be t₂ɡ⁶, eg³.

This configuration is similar to d¹ configuration in the sense that, there in is one hole in eg orbitals while other orbitals are filled. 

According to hole formalism, it is one hole system and show similar absorption spectra as that of d¹ system. If an electron excites from to eg, it may be considered as excitation of a hole from eg to t₂ɡ. Thus it is expected that the absorption spectrum show single line. However, a broad band formed by combination of three overlapping bands is observed. The absorption maxima is at 12,000 cm-¹ (833 nm) in aqueous solution and the colour is blue. 

Formation of three bands can be explained on the basis of Jahn-Teller effect. The eg orbitals are unsymmetrically filled and so the extent of distortion is large. Thus there electronic transitions are possible as shown in Figure.( Three possible extractions of electron or hole in [Cu(H₂O)₆]²+ ) and the Spectra is shown in Figure.(Absorption spectrum of[Cu(H₂O)₆]²+ ). Properties of band can be explained in the similar manner as that of hexaaquotitanium (III) Complex.