Origin of quantum mechanics
As it has been discussed earlier that the phenomenon like photoelectric effect, black body radiation,heat capacity and hydrogen spectrum could not be explained by classical mechanics. Max Planck assumed that the radiation consist of small packets of energy. It means that light has particle like nature. De-Broglie put forward an entirely new concept of dual nature of matter. He showed that matter consists of particles as well as wave associated with it. Schrodinger used this concept to develop a new theory called as 'Quantum Mechanics'.
The branch of science which takes into consideration de-Broglie concept of dual nature of matter and Planck's Quantum theory and is able to explain the phenomena related to microscopic particles is known as Quantum mechanics.
Comparison of Classical mechanics and Quantum mechanics
Classical mechanics deals with macroscopic particles while quantum mechanics deals with macroscopic particles.
Classical mechanics is based on Newton's laws of motion while quantum mechanics is based on de Broglie concept and Planck's quantum theory.
Classical mechanics is based on assumption that energy can be absorbed or emitted continuously while quantum mechanics believes that energy transition take place in discrete quanta.
The velocity of macroscopic particle is much less than velocity of light and so one can determine the position and velocity with large certainty. Thus, classical mechanics does not require the concept of probability. But quantum mechanics is applicable to microscopic particles moving with high velocities. Hence, Heisenberg's uncertainty principle plays important role and so the approach is based on probability.
Bohr's model of atom
Neils Bohr in 1913, proposed a theory of hydrogen atom which not only explained the origin of hydrogen spectrum but also led to an entirely new concept of atomic structure. His theory was based on some postulations of classical physics and some postulations of the newly proposed quantum theory of Planck. The important postulates on which Bohr's theory was based are discussed below.
An atom consists of a centrally located positively charged nucleus at which the entire mass of atom is concentrated. This postulate is same as Rutherford's model.
Electrons are revolving around the nucleus in fixed orbits of definite radii. The radius of nth Bohr orbit is given by-
rn= n²h²
4π²me²z
In a fixed orbit, the angular momentum of an electron is integral multiple of h/2π. That is,
Angular momentum=L=mvr=nh
2π
where,n is the principle quantum number.
Energy of electron is constant unless and until it is revolving in it's own shell. So, it neither absorbs nor emits energy unless and until it is in its own orbit or shell. Hence these orbits are called as stationary states or stationary energy levels. The energy of electron in nth energy level is given by
En =_ 13.6Z². eV
n²
When electron jumps from higher orbit to lower orbit, it radiates energy and when it jumps from lower orbit to higher orbit, it absorbs energy. The amount of energy absorbed or emitted is equal to the difference between electronic energy in the two orbits. The absorption or emission of energy takes place in the form of quanta.
∴ ∆E=E₂-E₁ =hv
Limitations of Bohr's model
Bohr's theory could very well explain the atomic spectra of hydrogen but failed to explain spectra of multielectron atoms.
When the atomic spectrum was observed under high resolution spectroscope, each single line was found to be a combination of a large number of closely spaced lines. This fine structure of spectrum could not be explained by Bohr's model.
Bohr's models assumes quantization of angular momentum and suggests that the angular momentum is integral multiple of h/2π. But it does not give any logical reasoning for this quantization.
Under the influence of electric field, the spectral lines split into groups of finer lines. This effect is called as Stark effect. This effect could not be explained by Bohr's model.
Similar to electric field, when atom is placed in magnetic field, the splitting of spectral lines takes place called as Zeeman effect. This could not be explained by Bohr's model.
Bohr assumed that electron is revolving in fixed orbit. But according to Heisenberg's uncertainty principle, it is not possible to determine position and velocity of electron simultaneously.
Dual nature of matter waves ( de Broglie hypothesis)
Main objections to Bohr's model are regarding quantization of angular momentum and uncertainty of position of electron. These difficulties were solved by Louis de Broglie in 1924. He suggested that all the material particles are associated with a wave. It means that each particle has dual nature, particle nature as well as wave nature. This wave is called as de-Broglie matter wave.
The mass and energy are related to each other by Einstein's equation.,
E= mc² -----------(1)
Also, according to Planck's quantum theory, energy of photon is given by,
E= hv ------------(2)
Combining equations (1) and (2) we get,
mc² = hv -------------(3)
But, frequency (v)= velocity ( c ).
wavelength(λ)
∴ mc² =hc/λ
∴ mc = h/λ or λ = h/m c ----------(4)
Substituting 'c' by the velocity of electron v,
Thus, the wavelength of material particle is given by,
λ = h/mv ----------(5)
But, mv= P (momentum)
∴ λ = h/P ----------(6)
This equation is known as de-Broglie equation.
It may be noted from equation (5) that wavelength is inversely proportional to the mass of particle. For big (macroscopic) particles, the mass is so large that the wavelength becomes too small to be measured. Hence larger particles do not show wave duality. However, microscopic particle like electron has negligible mass and so the wavelength becomes significant.
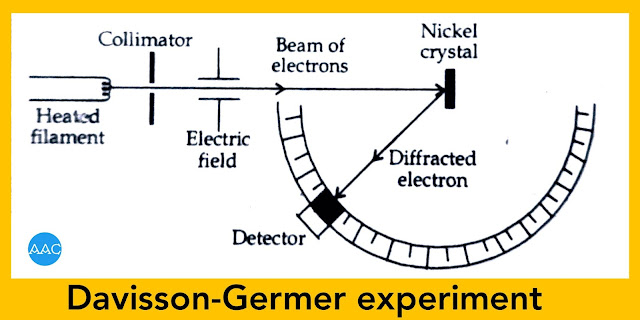
Experimental verification of de-Broglie concept (Davisson Germer experiment)
The experiment set up of Davisson Germer experiment is shown in Figure. Various steps involved in this experiment are as follows.
A sharp beam of electrons is obtained from heated filament which is accelerated by electric field. It is allowed to incident on a nickel crystal and intensity of diffracted electrons was determined at different angles using a detector.
Initially, accelerating potential is kept constant and the angle of detector was varied. It was observed that maximum intensity is obtained at an angle of 50°.
When this value of θ=nλ, the value of λ was found to be 1.65 Å for first order diffraction.
Then the angle was kept constant & accelerating potential was varied from 40 V to 68 V. It was observed that the maximum intensity obtains at 54V.
Now, momentum = P =√2eVm
Putting this value in de-Broglie equation λ=h/P, the value of λ was found to be1.66 Å.
Since the two values agree with each other, de-Broglie hypothesis is experimentally verified.
Heisenberg Uncertainty Principle
Calculation based on Bohr model can be carried out only if the position and velocity of an electron are accurately known. In 1972, Heisenberg's showed that there is a fundamental limit to the accuracy with which certain physical measurements may be made simultaneously. This limitation applies to many combinations of dynamical variables such as position,time,energy velocity, angular momentum etc. Consequently, it is not possible to take of the trajectory of an electron. On the basis of this Heisenberg put forward a principle which is known as Uncertainty principle.
According to Heisenberg's Uncertainty Principle, "it is not possible to measure simultaneously both the position and momentum (or velocity) of a small moving particle with absolute accuracy or certainty".
Mathematically, Heisenberg's uncertainty principle may be stated as "the product of uncertainty in position and momentum is always constant" and it can be expressed as-
∆x.∆P ≥ h/4π Where,∆x= Uncertainty in position
∆P= Uncertainty in momentum.
h= Planck's constant.
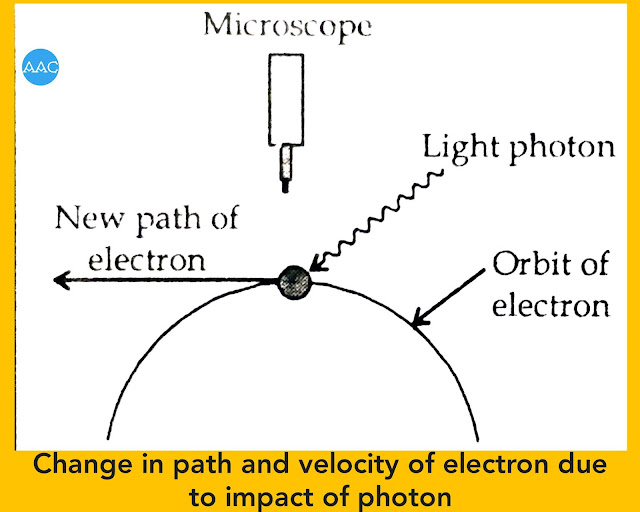
The ≥ sign indicates that the product of ∆x and ∆P can be either greater than or equal to h/4π. It means that if the position is determined exactly, the value of ∆x will decrease, but the value of ∆P will increase. Similarly, if momentum is determined exactly there will be large uncertainty in position. The reason behind this uncertainty can be understood if we consider the following figure.
It is known that, for locating any object, it is necessary that light photon should strike that object and enter the observing device. Due to impact of photon, particle like electron gets recoiled and velocity changes. Also the path of electron is altered.
Wave function
According to de Broglie hypothesis there is a wave associated with each matter particle. The amplitude function of the wave is called as wave function be noted by ψ. It is function of the variables x,y and z. Only those values of ψ are acceptable corresponding to definite amount of energy E. These values of E are called as eigen values and the wave function ψ is called as eigen function.
Well- behaved wave function
The eigen function is called as well-behaved wave function, it is fulfills following conditions-
ψ is single valued. That is, for each made of x,y,z,ψ must have only one definite value.
ψ is finite.
ψ is continuous. That is, there is no sudden change in the value of ψ.
The value of ψ vanishes to zero at infinity.
The physical significance of ψ has been established by Max Born suggested that ψ represent the amplitude of the wave associated with a matter particle like electron. However, in case of light or sound, square of amplitude gives intensity, similarly the square of the amplitude of electron wave (ψ²) gives the intensity of electron wave at that point. In other words,ψ² represent the probability density of an electron cloud and any point. It is also called as probability of finding an electron at that point.
Further, the value of ψ may be real or imaginary. But, probability cannot be taken as imaginary. Hence, for complex function, ψ ψ* is taken as probability instead of ψ². This is always real positive number. Here, ψ* is the complex conjugate of ψ.
Normalized wave function
Probability of finding a particle like electron in a small volume element dτ(=dx dy dz) is given by ψ ψ* dτ. The total probability of finding that particle over entire space is given by integrating this value between limits −∞ to +∞. This integration should we should come out to be 1.
+∞
∴ ∫ ψ ψ* dτ =1 ----------(1)
−∞
If this condition is fulfilled by the wave function, it is called as normalised wave function. In most of the cases, the value is not equal to 1, but it is equal to some constant N.
+∞ +∞
∫ ψ ψ* dτ =N ∴ 1/N ∫ ψ ψ* dτ =1
−∞ −∞
+∞
∴ ∫ (1/√N ψ) (1/√N ψ*) dτ =1
−∞
1/√N ψ is called as normalized wave function and 1/√N is called as normalization factor.
Orthogonal wave functions
If,for a given wave equation,there are two solutions given by normalized wave functions ψm and ψn, then they are said to be orthogonal wave functions if
+∞ +∞
∫ ψmψ*n dτ =0 and ∫ ψm* ψn dτ =0 ------(2)
−∞ −∞
Orthonormal wave functions
If two wave functions are normalised as well as orthogonal, they are said to be orthonormal wave functions. They satisfy equation (1) and (2).
Introduction of operators eigen value and eigen functions
An operator is a mathematical instruction or procedure to be carried out on a function to transform it into another function. In general, the operation can be written as
(Operator).(Function)=(Another function)
The commonly used operators are differentiation and integration. For example,
d/dx (x²) = 2x
In this equation, d/dx is called as operator, x² is called as function and 2x is the new function.
If it is possible to express the new function as a product of old function and some constant, then such function is called as eigen function and a constant multiple is called as eigen value of the operator. For example,
5x 5x
d (e ) = 5e
dx
5x
In this case,e is called as eigen function and 5 is called as eigen value of the operator d/dx.
Postulates of quantum mechanics
The entire quantum mechanics is based on five basic postulates. These are follows-
For every independent state of system, a function ψ can be written which describes the state of the system completely. It is single valued continuous and finite throughout configuration space.
To each observable quantity in classical mechanics, like position, velocity, momentum, energy etc, there exist a mathematical operator in quantum mechanics. Some of the operators are given below.
Note: x̂ is pronounced as x-cap,P̂x as Px - cap etc.
If ψ is well behaved wave function and  is a suitable operator for the observable quantity or property, then the operation on ψ by the operator  gives ψ multiplied by a constant value of the observable property. It is eigen value of operator
That is, Âψ = aψ
The only possible measured values open observable are the eigen values obtained from the eigen value equation given by equation Âψ = aψ.
If a number of measurements are made over the configuration space, then the average value of the quantity is given by
ā = ∮ψ* Âψdτ / ∮ψ* ψdτ
Derivation of Schrodinger's wave equation from postulates of quantum mechanics
Consider a single electron having mass 'm' moving with a velocity 'v'. The total energy of this electron is the sum of kinetic energy (T) and potential energy (V). ∴ E = T + V
From classical mechanics, kinety energy is given by, T = ½ mv² = P²/2m
Further the total momentum P can be resolved into three mutually perpendicular vectors as
P² = Px² + Py² + Pz²
∴ T = Px² + Py² + Pz²
2m
∴ E = Px² + Py² + Pz² + V
2m
From second postulate of quantum mechanics
P̂²x = −h² ∂² . and E =Ĥ (Hamiltonian operator of energy)
4π² ∂x²
The Hamiltonian operator Ĥ is given by-
∴ Ĥ =1/2m[(-h²/4π². ∂²/∂x²)+(-h²/4π². ∂²/∂y²)+(-h²/4π². ∂²/∂z²)]+V
∴ Ĥ =-h²/8π²m [∂²/∂x²+∂²/∂y²+∂²/∂z²]+V
∴ Ĥ =-h²/8π²m· ∇²+V
∇ is called Laplacian operator and ∇²=∂²/∂x²+∂²/∂y²+∂²/∂z²
According to third postulate of quantum mechanics,
Ĥψ= Eψ
∴ Ĥψ - Eψ =0
∴ (-h²/8π²m· ∇²+V)ψ-Eψ=0
∴ ∇²ψ+8π²m/h².(E-V)ψ=0 ------------(1)
This is the common form of Schrodinger's wave equation. It can also be put in the form
∂²ψ/∂x²+∂²ψ/∂y²+∂²ψ/∂z²+8π²m/h².(E-V)ψ=0 ----------(2)
Applications of Schrodinger wave equation to particle in one dimensional box
Consider a particle of mass 'm' in one dimensional box of length 'a'. The potential energy of particle in the box is 0 while outside the box, it is ∞. Schrodinger wave equation is given by
d²ψ/dx²+8π²m/h².(E-V)ψ=0 ------------(1)
Outside the box, the potential energy is ∞, hence
∴ d²ψ/dx²-8π²m/h².(∞)ψ=0
∴ ψ=1/∞. h²/8π²m .d²ψ/dx²
∴ ψ=0
Hence, wave function is zero outside the box. Inside the box, the potential energy V is 0. Hence,
d²ψ/dx²+8π²mE/h² .ψ = 0
According to postulates of quantum mechanics, for a given state of a system, energy E is constant.
∴ 8π²mE/h² = constant = k² -------------(2)
where, k² is constant independent of x.
∴ d²ψ/dx²+k²ψ=0 ------------(3)
This is equation of simple harmonic motion having solution
ψ= A sin kx + B cos kx -------------(4)
For calculating the values of A, B and k, we apply boundary conditions in equation (4).
At x= 0 , ψ=0
∴ 0= A sin 0 + B cos 0
∴ 0= A× 0 + B × 1
∴. 0= B or B= 0
So, equation (4) becomes
ψ= A sin kx --------------(5)
At x = a, ψ= 0
Hence equation (5) becomes 0 = A sin ka
So, either A = 0 or sin ka = 0
But A can not be 0 because if A is 0, total ψ will become 0
∴ sin ka = 0
∴ ka = nπ where, n= 0,1,2,----
∴ k= nπ / a -----------------(6)
Putting in equation (5) we get,
ψ= A sin(nπ/a.x) ----------------(7)
This equation gives the value of wave function ψ.
Normalization of wave function
According to definition of normalized wave function,
+∞
∫ ψψ* dτ =1
−∞
But the probability of finding the particle outside the box is zero. So, the entire probability is inside the box. Hence the equation becomes-
a
∫ ψψ* dτ =1
0
Putting values of ψ and ψ* (which are equal) from equation
a
∫ A² sin² (nπ/a.x) dτ =1
0
a
∴ A² ∫ sin² (nπ/a.x) dτ =1
0
∴ A² (a/2)=1
(This value can be obtained by using equation sin²x=1-cos2x and then solving the above integration)
∴ A=√2/a
Putting in equation of ψ, we get
ψ=√2/a .sin (nπx/a)
Energy of particle in one dimensional box
From equation (2), we have
∴ 8π²mE/h² = k²
Putting value of k, we get
∴ E= k²h²/8π²m = (nπ/a)².h² / 8π²m = n² h²/8ma² --------(8)
This equation shows that the values of energy of particle in one dimensional box are quantized.
Since 'n' has only integral values, the energy values are given as follows-
For n=1, E= h²/8ma²
For n=2, E= 4h²/8ma²
For n=3, E= 9h²/8ma²
The minimum energy corresponding to n= 1 is called as zero point energy. It is given by-
ψ=√2/a .sin (nπx/a)
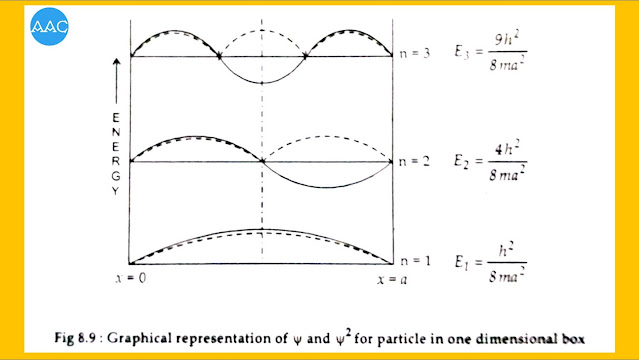
Putting values of n= 1,2,3-----etc we can plot graphs of ψ as a function of position x. Similarly, the ψ² gives the probability of finding the particle.
For n=1, ψ₁=√2/a .sin (πx/a).
This value becomes 0 at x=0 and x=a. It is maximum at x= a/2. Thus the probability ψ² is maximum at x= a/2. It means that the particle is most likely to be found at the centre of the box if it is in ground state n=1.
For n=2, ψ₂=√2/a .sin(2πx/a).
This value becomes zero at x=0, x=a/2 and x=a. It is maximum at x= a/4 and minimum at x=3a/4 (negative). Thus the probability ψ² is maximum at x= a/4 and x=a/4 and x=3a/4. It means that the particle is most likely to be found at the centre of the two halves if it is in first excited state n=2. The point of zero probability at x=a/2 is called as node.
For n=3, ψ₃=√2/a .sin(3πx/a).
This value becomes zero at x=0, x=a/3, x=2a/3 and x=a. So,it has two nodes.
Various wave functions and probability distribution curves are shown in Fig 8.9. Number of nodes in any state is given by n-1.
It can be seen that, if an imaginary plane is passed through the center of the box, the wave function ψ₁ is symmetrical about the plane. ψ₂ is antisymmetric about the plane. In the similar manner, all the odd wave functions are symmetrical while even wave functions are antisymmetrical.
Applications of particle in one dimensional box
Quantization of energy:
According to the equation of energy of particle in one dimensional box, the energy is given by E=n²h²/8ma².
Here, n is the principal quantum number which has values n=1,2,3---. If we put these values,
For n=1, E=h²/8ma²
For n=2, E=4h²/8ma²
For n=3, E=9h²/8ma²
It clearly shows that the energy of particle is quantized.
Zero point energy:
According to the equation of energy of particle in one dimensional box, the energy is given by E=n²h²/8ma². The value of n starts from n=1. For this value, the minimum energy associated with particle is given by E=h²/8ma². This is called as zero point energy. This energy is associated with the particle even at 0 K temperature.
Non-quantization of energy:
If a particle is set free by removing barriers of potential well, the energy of particle becomes E= k²h²/8π²m. Since k is not quantized, the energy is not quantized. Hence,a free particle can have continuous values of energy.












0 comments:
Post a Comment